General physics 1

Learning Outcomes

On completion of the course, the student should be able to:

1.    identify and deduce the physical quantities and their units;

2.    differentiate between vectors and scalars;

3.    describe and evaluate motion of systems on the basis of the fundamental laws of mechanics;

4.    apply Newton’s laws to describe and solve simple problems of motion;

5.    evaluate work, energy, velocity, momentum, acceleration, and torque of moving or rotating objects;

6.    explain and apply the principles of conservation of energy, linear and angular momentum;

7.    describe the laws governing motion under gravity; and

8.    explain motion under gravity and quantitatively determine behaviour of objects moving under gravity.

Course Contents

space and time. units and dimension. vectors and scalars. differentiation of vectors: displacement, velocity and acceleration. Kinematics. Newton laws of motion (Inertial frames, Impulse, force and action at a distance, momentum conservation). relative motion. Application of Newtonian mechanics. equations of motion. conservation principles in physics, conservative forces, conservation of linear momentum, Kinetic energy and work, Potential energy, System of particles, Centre of mass. Rotational motion. torque, vector product, moment, rotation of coordinate axes and angular momentum, polar coordinates. conservation of angular momentum; Circular motion. Moments of inertia, gyroscopes and precession. gravitation: Newton’s Law of Gravitation, Kepler’s Laws of Planetary Motion, Gravitational Potential Energy, Escape velocity, Satellites motion and orbits.

PART A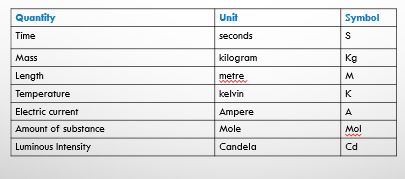
•Space and Time: Units and dimension
•Vector and scalar:
•differentiation of vectors: displacement, velocity and acceleration
•Kinematics: Newton’s law of motion
•Relative motion
•Applications of Newtonian mechanics
•Equation of MOTION
•Conservation principles in physics: conservative forces, conservation of linear momentum, kinetic energy and work, potential energy

In Physics any quantity that has a measurable property is known as a physical quantity. Physical quantity can be classified into two: fundamental and derived quantity. 
Fundamental quantities are independent quantities or that do not depend on any other quantities for their derivations and their units are called fundamental units. Examples are
                                    

Derived quantities are those quantities that derived from the fundamental quantities. Their units are known as derived units. Examples are:

                                     

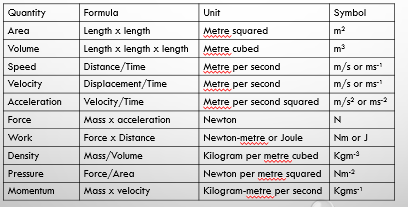
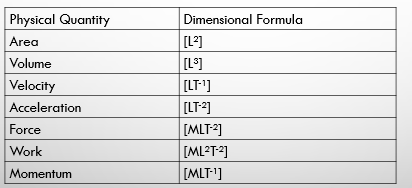
DIMENSION:  Dimensions are the powers to which fundamental quantities are raised to represent a particular quantity.
                                     
                                         

Uses of dimensions:
•To determine the true relationship between physical quantities
•Helps to determine the appropriate unit of a physical  quantity
•To check the accuracy of physical quantities.
                                        
                                       
                                  
SCALAR AND VECTOR QUANTITIES
•Scalar is a quantity with magnitude but no direction. E.g. distance, time, temperature, area, volume, electric current, energy, speed e.t.c.
•Vector is a quantity with both magnitude and direction. E.g displacement, force, velocity, acceleration, momentum etc.

Vector resolution:   Vectors can be resolved into: vertical and horizontal components
 
Vector direction:   In 2-D, the angle that vector A makes with the positive  x-axis is given as:
                                                               
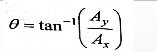
Unit vector:  A unit vector is a vector having a unit magnitude. It is used to describe the direction of the vector. It is given as:
                                 
                                

                            
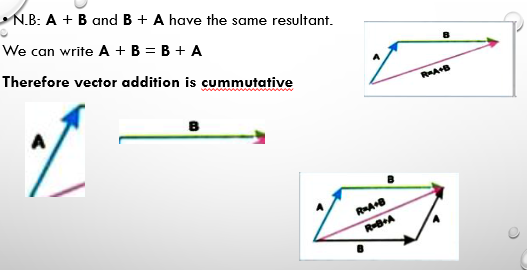
VECTOR ADDITION:  The process in which to or more vectors are added to get a single vector is called vector addition. This single vector is known as resultant vector. It has the same effect as the other vectors combined together.
Vectors can be added graphically by head to tail rule. According this rule, addition of vector A and B can be done by
1.Placing the tail of B on the head of A
2.Drawing a line from the tail of A to the head of B. is line is the sum of vectors A and B called the resultant vector.
                              
•Vectors can also be added component-wisely
 e.g Two vectors A and B are give as A = 2i + 3j + 2k and B = i + 2j + 4k. Find the value of A +B
Solution

Given: A = 2i + 3j + 2k , B = i + 2j + 4k.

A +B =  (2i + 3j + 2k )+  (i + 2j + 4k)

Adding i to i, j to j and k to k

= 2i +i + 3j + 2j +2k + 4k

= 3i + 5j + 6k

N.B: Addition of vector gives a vector

                    

2